Proof generation phase

This section explains the proof generation phase for all proofs; the zkEVM STARK, the compression c12a step, the recursion proof recursion1, the intermediate recursion proof recursion2 and the final recursion proof recursionf.

Proof of the zkEVM STARK¶

The execution trace has up to this point been built, together with a PIL file describing the ROM of the zkEVM. Given these two, a STARK proof which attests to the correct execution of the zkEVM, can be generated using the PIL-STARK tooling explained here.

In this step, a blowup factor of 2 is used, so the proof becomes quite big due to a huge amount of polynomials.

The compression step c12a was added for this very reason, raising the blowup factor and thus reducing the number of polynomials.

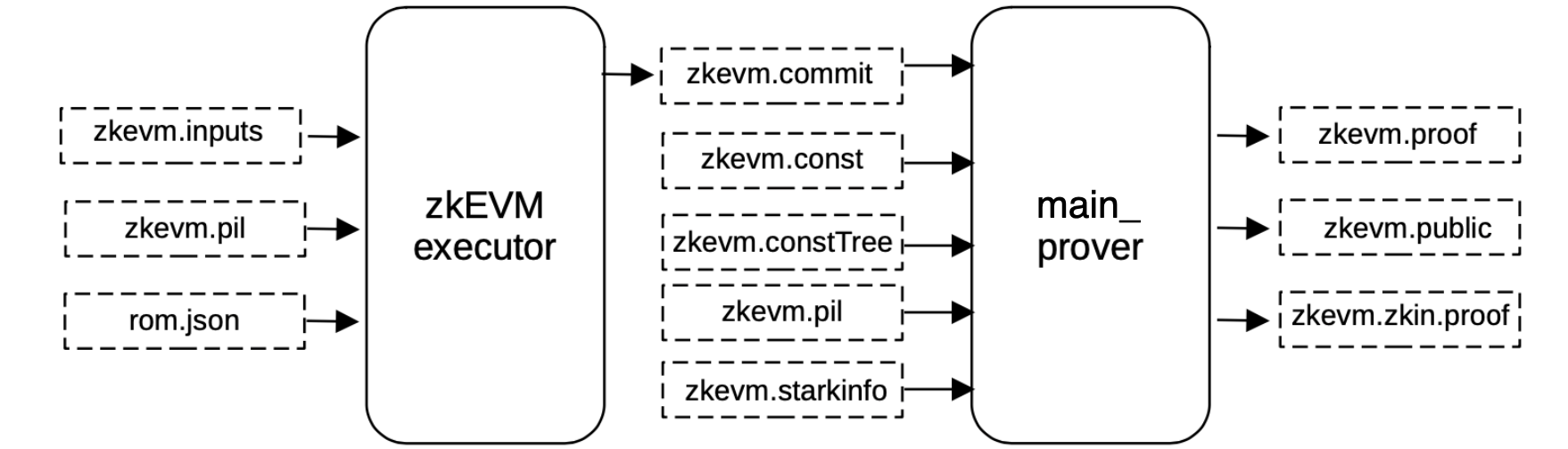
Generation for a zkEVM Proof.

In order to generate the proof, the \(\mathtt{main\_prover}\) service is used, and requires as input;

the execution trace (that is, the committed and constant polynomials files generated by the executor using the PILCOM package),
the constant tree binary file in order to be hashed to compute the constant root,
the PIL file of the \(\text{zkEVM ROM}\) zkevm.pil, and
all the information provided by the zkevm.starkinfo.json file,

including all the FRI-related parameters such as the blowup factor or the configuration of the steps.

This step is intended to start the recursion, and therefore differs from the subsequent ones. However, aiming at uniformity of the code, the Main Prover procedure chooses to abstract the notion of proving. And it is intended to be the same at each step of the recursion.

Proof of c12a¶

In order to generate the proof verifying the previous zkevm.proof, all the witness values can be generated and mapped correctly into its corresponding position of the execution trace in the same exact manner as before, obtaining a binary file c12a.commit for the committed polynomials of the execution trace.

Having the execution trace (that is, the committed and constant polynomials filled) and the PIL, a proof validating the previous big STARK proof can be generated.

The same \(\mathtt{main\_prover}\) service used earlier is again used here, and as before it takes as input the previously built constant tree c12a.constTree and the c12a.starkinfo file.

It in turn generates the proof c12a.proof and the publics c12a.public combined in the c12a.zkin.proof file.

Generate a STARK proof for c12a.

Proof of recursive1¶

In order to generate the proof that verifies the previous c12a.proof, all the witness values are generated and mapped correctly into their corresponding positions of the execution trace in the exact same way as before, obtaining a binary file recursive1.commit for the committed polynomials of the execution trace.

Having the execution trace (that is, the committed and constant polynomials filled) and the PIL, a proof validating the previous big STARK proof can be generated.

The same \(\mathtt{main\_prover}\) service used previously is applied again here, it again takes as input the previously built constant tree recursive1.constTree and the recursive1.starkinfo file.

This generates the proof and the publics joined in the recursive1.zkin.proof file.

Generate a STARK proof for recursive1.

Proof of recursive2¶

To generate the proof verifying the previous recursive1.proof, all witness values must be generated and mapped correctly into their corresponding positions of the execution trace in the exact same way as before, obtaining a binary file recursive2.commit for the committed polynomials of the execution trace.

Having the execution trace (that is, the committed and constant polynomials filled) and the PIL, a proof validating the previous big STARK proof can generated.

The same service \(\mathtt{main\_prover}\) generates this proof, as it was done before, it takes as inputs the previously built constant tree recursive2.constTree and the recursive2.starkinfo file.

This generate the proof and the publics combined in the recursive2.zkin.proof file.

Generate a STARK proof for recursive2.

Proof of recursivef¶

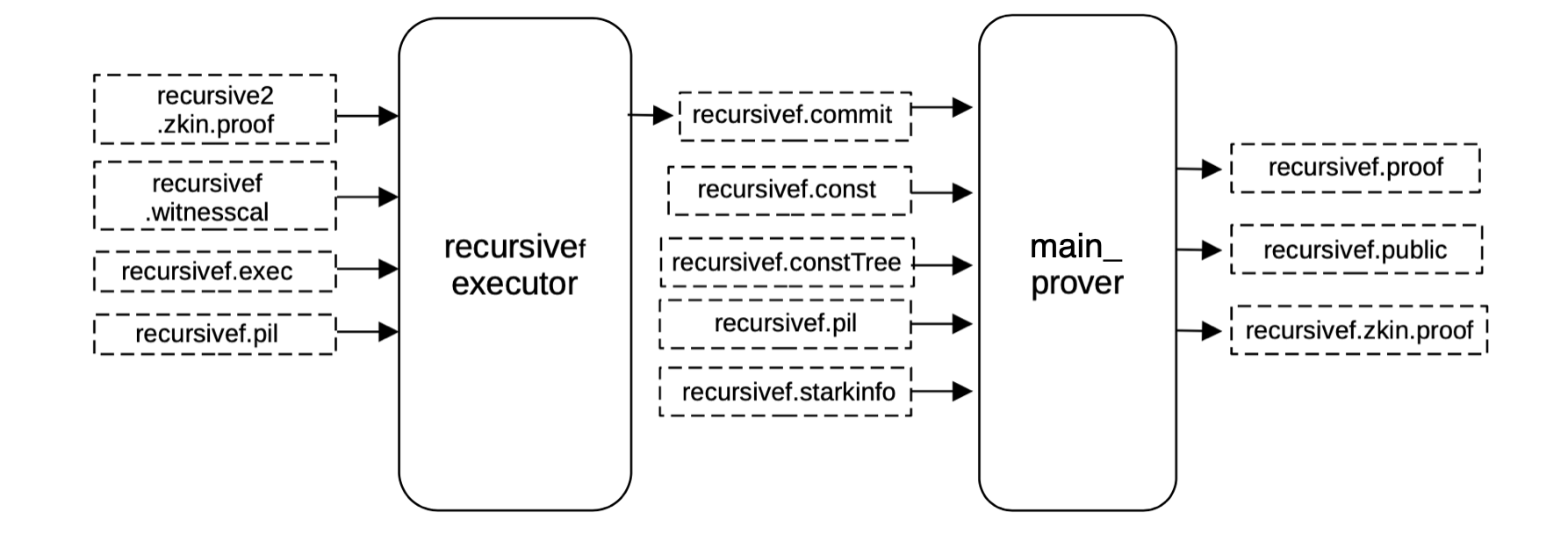
To generate the proof verifying the previous recursive2.proof, we generate all the witness values and map them correctly into its corresponding position of the execution trace exactly in the same way as before, obtaining a binary file recursivef.commit for the committed polynomials of the execution trace.

Having the execution trace (that is, the committed and constant polynomials filled) and the PIL, we can generate a proof validating the previous big STARK proof.

Again, the same \(\mathtt{main\_prover}\) service is used to generate the proof. As before, it takes as inputs the previously built constant tree \(\mathtt{recursivef.constTree}\) and the \(\mathtt{recursivef.starkinfo}\) file.

This will generate the proof and the publics joined in the recursivef.zkin.proof file.

Generate a STARK proof for recursivef.

Proof of the final Stage¶

The last circuit, final.circom is the one used to generate the proof. At this moment a FFLONK proof is generated.

Remarks¶

The setup phase runs with the proverjs. The proof generation runs with the prover written in \(\text{C}\). The circuits build in the setup phase can be used as many times as desired. The prover receives the information about the particular composition of proofs with an \(\text{RPC}\) \(\text{API}\).