Skip to main content
The Bits2Field state machine is one of the auxiliary state machines used specifically for parallelizing the implementation of KECCAK-F SM. Its source code is available here. The Bits2Field state machine ensures correct packing of 44\mathtt{44} bits from 44\mathtt{44} different 1600\mathtt{1600}-row blocks of the Padding-KK-Bit SM into a single field element. Therefore, it operates like a (44-bits-to-1-field-element) multiplexer between the Padding-KK-Bit SM and the Keccak-F SM. In simpler terms, it takes bits from 44\mathtt{44} different blocks, places them into the first 44 bit-positions of a single field element, whereupon the KECCAK-F circuit runs. The name Bits2Field state machine refers to the process of taking 4444 bits from 4444 different blocks of the Padding-KK-Bit SM and inserting them into a single field element. Although the KECCAK-F SM is a binary circuit, instead of executing on a bit-by-bit basis, it is implemented to execute KECCAK-F operations on a 44bits-by-44bits basis. This is tantamount to running 44\mathtt{44} KECCAK-F hashing circuits in parallel. The figure below depicts a simplified multiplexing process. 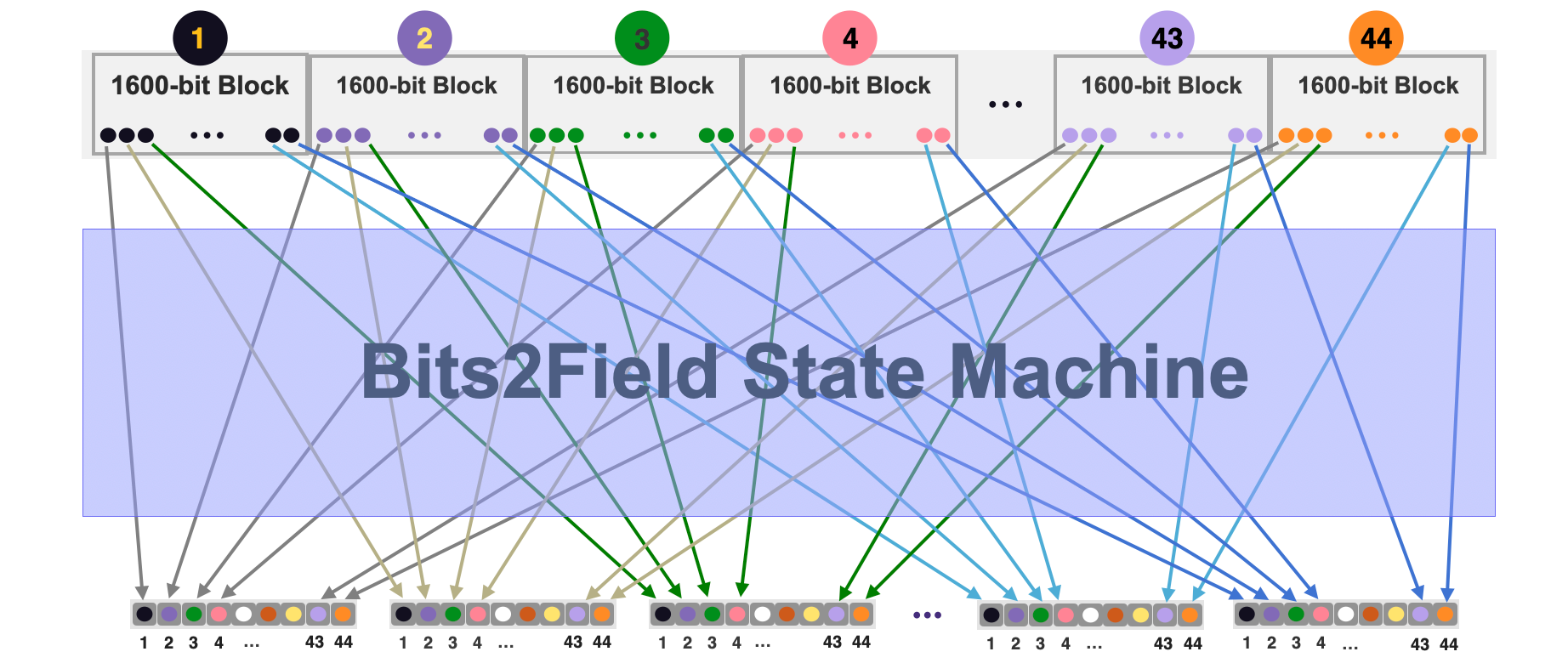The 44 bits to 1 field-element Multiplexing

​
Mapping 44 Bits To A 64-bit Field Element

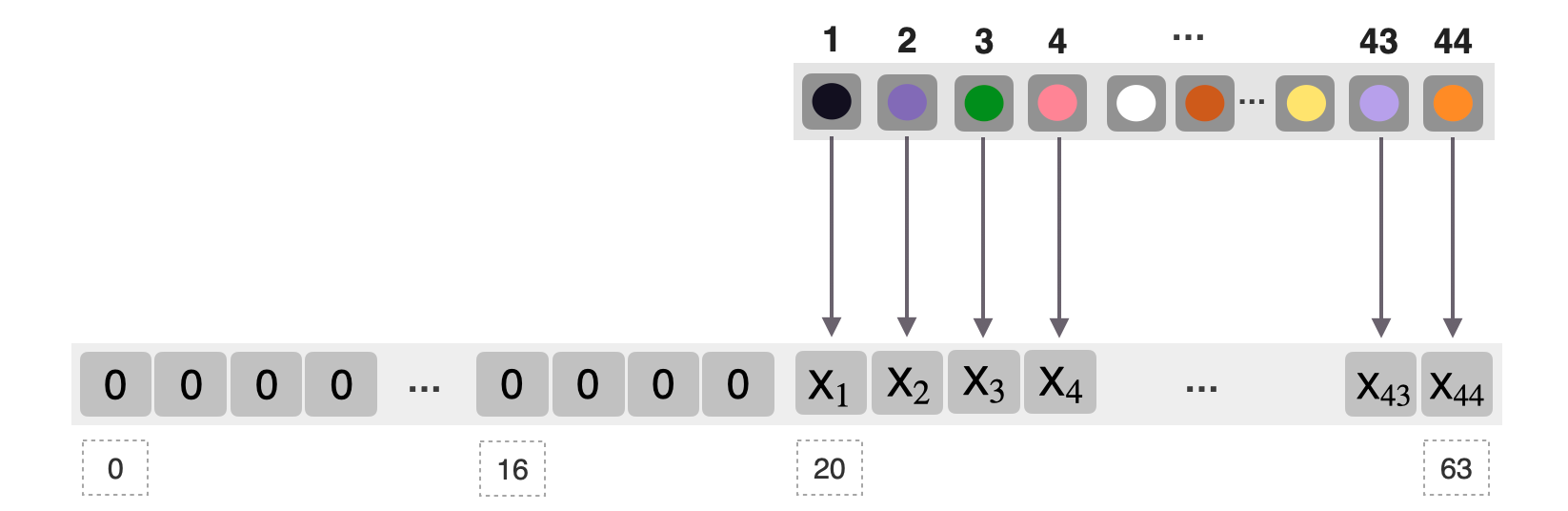
Suppose operations are carried out in a field Fp\mathbb{F}_p of 64\mathtt{64}-bit numbers. The smallest field used in the zkProver is the Goldilocks Field Fp\mathbb{F}_p where p=264−232+1p = 2^{64} - 2^{32}+1. After multiplexing, the 44 bits are loaded into the first 44 least significant bit-positions of the field element as depicted in the figure below. Figure 2: 44 Bits mapped to a 64-bit field element A field element as an input to the KECCAK-F circuit is of the form, 0b0000 0000 0000 0000 0000 X1X2X3X4 X5X6X7X8 …X43X44 \mathtt{0b}\mathtt{0000\ 0000\ 0000\ 0000\ 0000}\ \mathtt{X}_1 \mathtt{X}_2 \mathtt{X}_3 \mathtt{X}_4\ \mathtt{X}_5 \mathtt{X}_6 \mathtt{X}_7 \mathtt{X}_8\ \dots \mathtt{X}_{43} \mathtt{X}_{44} \text{ } and it is composed of 20 zeroes and 44 meaningful bits related to the committed polynomials. Given the capacity of 2232^{23} in terms of the state machine evaluations (i.e., the degree of polynomials) and the KECCAK-F’s SlotSize=155286\texttt{SlotSize} = 155286, one obtains 223/155286=54.0203753072^{23} / 155286 = 54.020375307 KECCAK-F slots. Therefore, a total of 5454 slots ×\times 4444 blocks =2376= 2376 Keccak blocks can be processed. This is a big improvement from the previous 477477 blocks of the 9bits-to-1field element multiplexing (i.e., 53×9=47753 \times 9 = 477).

​
The Bits2Field PIL Code

The Bits2Field executor executes the multiplexing of forty-four 1600\mathtt{1600}-bit blocks into 1600\mathtt{1600} field elements, where each is a N\mathtt{N}-bit field element. For reference, see the above figure where N=64\mathtt{N = 64}. The question here is how to identify each of the original 9 bits of the field element to track their corresponding resultant XOR\mathtt{XOR} values or ANDP\mathtt{ANDP} values? Note that every bit bi,j\mathtt{b_{i,j}} from the i\mathtt{i}-th 1600\mathtt{1600}-bit block is placed at the 2‘i‘\mathtt{2^`{i}`}-th position of the N\mathtt{N}-bit field element. The PIL code therefore uses factors denoted by Factor\mathtt{Factor}, such that Factor∈{1,2,4,…,243}\mathtt{Factor \in \{ 1, 2, 4, \dots , 2^{43} \}}, and a Fieldlatch\mathtt{Fieldlatch} after running through forty-four 1600\mathtt{1600}-bit blocks. Suppose N=64\mathtt{N = 64}. Then the 44 least significant bits of the 64\mathtt{64}-bit field element looks like this: field44=X1⋅243+X2∗242+X3∗241+⋯+X42∗22+X43∗2+X44.\mathtt{field44 = X_1 \cdot 2^{43} + X_{2}*{2}^{42} + X_{3}*{2}^{41} + \dots + X_{42}*{2}^2 + X_{43}*2 + X_{44}}. The constraint checked is therefore, field44′=(1−Fieldlatch)∗field44+bit∗Factor\mathtt{field44' = (1-Fieldlatch)*field44 + bit*Factor} The accumulated field element at the end of the execution (every forty-fourth row of the execution trace) is checked against the KECCAK-F input KeccakF.a\mathtt{KeccakF.a} with the boundary constraint, Fieldlatch∗(field44−KeccakF.a)=0\mathtt{Fieldlatch*(field44 - KeccakF.a) = 0} The PIL code is given below. 
% "bits2field.pil"

include "keccakf.pil";

namespace Bits2Field(%N);
    pol constant FieldLatch;  // [0:44,1]
    pol constant Factor;  // 1,2,4,8,...,2**43

    pol commit bit;
    pol commit field44;

    field44' = (1-FieldLatch)*field44 + bit*Factor;
    bit *(1-bit) = 0;

    FieldLatch*(field44 - KeccakF.a44) = 0;